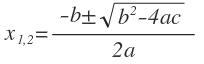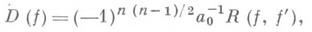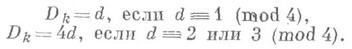Что обозначает слово дискриминант
Дискриминант
квадратного уравнения
Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.
Вернемся к нашей формуле для нахожденя корней квадратного уравнения.
Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».
В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
I случай
D > 0
(дискриминант больше нуля)
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| −5 ± √ 81 |
| 2 · 2 |
x1;2 =
| −5 ± 9 |
| 4 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 1 | x2 = −3
| ||||
| x1 = 1 | x2 = −3
|
Ответ: x1 = 1; x2 = −3
| 1 |
| 2 |
II случай
D = 0
(дискриминант равен нулю)
D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| − (−8) ± √ 0 |
| 32 |
x1;2 =
| 8 ± 0 |
| 32 |
x =
| 8 |
| 32 |
x =
| 1 |
| 4 |
Ответ: x =
| 1 |
| 4 |
III случай
D
(дискриминант меньше нуля)
D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| − (−6) ± √ −36 |
| 32 |
Ответ: нет действительных корней
дискриминант
Полезное
Смотреть что такое «дискриминант» в других словарях:
ДИСКРИМИНАНТ — перекись твою Ньютона! Жарг. студ. Бран. шутл. Выражение досады, раздражения. Вахитов 2003, 48 … Большой словарь русских поговорок
дискриминант — а, м. discriminant m. <лат. discriminare разделять, отделять. мат. Составленное из величин, определяющих заданную функцию. выражение, обращением которого в нуль характеризуется то или иное отклонение функции от нормы, напр. д. многочлена равен … Исторический словарь галлицизмов русского языка
дискриминант — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN discriminant … Справочник технического переводчика
дискриминант — квадратного уравнения ах2 + bx + с = 0, выражение b2 – 4ас = D, по знаку которого судят о наличии у этого уравнения действительных корней (D≥0). * * * ДИСКРИМИНАНТ ДИСКРИМИНАНТ квадратного уравнения ax2 + bx + c = 0 выражение b2 – 4ac = D, по… … Энциклопедический словарь
дискриминант — diskriminantas statusas T sritis fizika atitikmenys: angl. discriminant vok. Diskriminant, m rus. дискриминант, m pranc. discriminant, m … Fizikos terminų žodynas
Дискриминант — (от лат. discriminans разделяющий, различающий) многочлена P (x) = a0xn + a1xn 1 +. + an, выражение D = a02n 2Пi … Большая советская энциклопедия
дискриминант — дискриминант, дискриминанты, дискриминанта, дискриминантов, дискриминанту, дискриминантам, дискриминант, дискриминанты, дискриминантом, дискриминантами, дискриминанте, дискриминантах (Источник: «Полная акцентуированная парадигма по А. А.… … Формы слов
Как найти дискриминант квадратного уравнения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие квадратного уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.
Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.
Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Есть три вида квадратных уравнений:
Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.
Чаще всего для поиска дискриминанта используют формулу:
В этом ключе универсальная формула для поиска корней квадратного уравнения выглядит так:
Эта формула подходит даже для неполных квадратных уравнений.
Но есть и другие формулы — все зависит от вида уравнения. Чтобы в них не запутаться, сохраняйте табличку или распечатайте ее и храните в учебнике.
Как решать квадратные уравнения через дискриминант
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!
Примеры решения квадратных уравнений с помощью дискриминанта
Ответ: корень уравнения 3.
Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.
Значение слова «дискриминант»
1. матем. функция коэффициентов многочлена, позволяющая определить его корни
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: пождать — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «дискриминант»
Предложения со словом «дискриминант»
Понятия, связанные со словом «дискриминант»
Отправить комментарий
Дополнительно
Предложения со словом «дискриминант»
Значит, дискриминант равен 841 под квадратным корнем.
К примеру, отрицательный дискриминант свидетельствует о том, что квадратное уравнение не имеет решений.
Примерно так, как это преподносит нам дискриминант квадратного уравнения.
Синонимы к слову «дискриминант»
Морфология
Правописание
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
ДИСКРИМИНАНТ
Д. равен нулю тогда и только тогда, когда многочлен имеет кратные корни. Д. симметричен относительно корней многочлена и поэтому может быть выражен через его коэффициенты.
Лит.:[1] Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975.
Пусть k=Q— поле рациональных чисел, К- поле алгебраич. чисел и М- некоторый модуль ранга пв К. Тогда для любых двух базисов модуля Мзначения Д. совпадают и это общее значение Д. наз. дискриминантом модуля М. Если Мсовпадает с кольцом целых чисел поля К, то Д. модуля Мназ. просто дискриминантом поля К и обозначается Dk. Число Dk, является важной характеристикой поля К. Напр., если Кдопускает s вещественных и 2t комплексных вложений в поле комплексных чисел С, то
где zk(q)- дзета-функция Дедекинда, h- число классов дивизоров, R— регулятор поля К и т— число корней из единицы в поле К. Имеется оценка
которая показывает, что 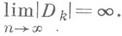
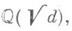
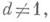
Лит.:[1] Боревич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; [2] Ленг С, Алгебраические числа, пер. с англ., М., 1966; [3] 3арисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1963; [4] Джекобсон Н., Теория колец, пер. с англ., М., 1947.
Лит.:[1] Джекобсон Н., Теория колец, пер. с англ., М., 1947.