Что значит слово динамика
Значение слова «динамика»
1. Раздел механики, изучающий законы движения тел в зависимости от действующих на них сил.
[От греч. δυναμικός — действующий]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Системная динамика — направление в изучении сложных систем.
ДИНА’МИКА, и, мн. нет, ж. [от греч. dynamikos — действующий]. 1. Отдел механики, изучающий законы движения тел в зависимости от действующих на них сил (мех.). 2. Ход развития, изменения какого-н. явления под влиянием действующих на него сил; противоп. статика во 2 знач. (науч.). Д. социального процесса. 3. перен. Обилие движения, действия (книжн.). В пьесе много динамики.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
дина́мика I
1. физ. раздел механики, изучающий движение тел под воздействием сил
2. состояние развития, движения
3. развитие, движение ◆ — Состояние тяжёлое, — пояснил врач, — но динамика положительная. Татьяна Устинова, «Большое зло мелкие пакости», 2003 г. (цитата из НКРЯ)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: транспарант — это что-то нейтральное, положительное или отрицательное?
Значение слова динамика
Словарь Ушакова
1. Отдел механики, изучающий законы движения тел в зависимости от действующих на них сил (мех.).
2. Ход развития, изменения какого-нибудь явления под влиянием действующих на него сил; ант. статика во 2 знач. (научн.). Динамика социального процесса.
3. перен. Обилие движения, действия (книж.). В пьесе много динамики.
Педагогическое речеведение. Словарь-Справочник
(греч. dinamys — сила)
1) движение, развитие, изменение какого-либо явления под влиянием действующих на него факторов;
2) (спец.) совокупность степеней силы звучания, громкости.
Лит.: Бондарко Л.В. Звуковой строй современного русского языка. — М, 1977; Романовский Н.В. Хоровой словарь. — М., 1980; Словарь иностранных слов. — М., 1984.
Начала Современного Естествознания. Тезаурус
(от греч. dynamis — сила, dynamikos — относящийся к силе, сильный)
1) раздел механики, изучающий движение тел под действием сил, согласно законам динамики Ньютона;
2) состояние движения, ход развития, изменение чего-либо под влиянием действующих на него факторов (противоположность — статика);
3) обилие движения, действия;
4) (в музыке) различные степени силы звучания, громкости и их изменения, обозначаемые итальянскими терминами: пиано — тихо, форте — громко, крещендо — постепенно усиливая, диминуэндо — постепенно затихая и др.
Справочный Коммерческий Словарь (1926)
движение; в переносном смысле — последовательное развитие какого-либо явления, в статистике под динамикой подразумевают изображение такого развития в относительных числах; напр. «динамика» движения оборотов за 4 квартала года (приняв оборот 1-го квартала за 100): 100, 125, 135, 150.
Словарь антонимов русского языка
Словарь музыкальных терминов
(от гр. dynamikos — силовой) — сила (громкость) музыкального звучания. Основные обозначения динамики: f (forte — форте) — громко, сильно; р (piano — пиано) — тихо, слабо; mf (mezzo-forte — меццо-форте) — умеренно громко; mp (mezzo-piano — меццо-пиано) — умеренно тихо; рр (pianissimo — пианиссимо) — очень тихо; ff (fortissimo — фортиссимо) — очень громко и т. д. Постепенное увеличение силы звучания — крешендо ( cresc. ); постепенное ослабление — диминуэндо ( dim. ). Динамика является важным выразительным средством, влияющим на восприятие музыки, вызывающим разнообразные ассоциации. Использование динамических оттенков обусловливается содержанием и характером музыки, особенностями ее структуры и стиля. Логика соотношения музыкальных звучностей — одно из основных условий художественного исполнения.
Тезаурус русской деловой лексики
Энциклопедический словарь
Словарь Ожегова
ДИНАМИКА, и, ж.
1. Раздел механики, изучающий движение тел под действием приложенных к ним сил.
2. Ход развития, изменения какогон. явления (книжн.). Д. общественного развития.
3. Движение, действие, развитие. В пьесе много динамики.
| прил. динамический, ая, ое (ко 2 знач.).
Динамика
Дина́мика (от греч. dynamikós — сильный, от dýnamis — сила)
раздел механики (См. Механика), посвящённый изучению движения материальных тел под действием приложенных к ним сил. В основе Д. лежат три закона И. Ньютона (см. Ньютона законы механики), из которых как следствия получаются все уравнения и теоремы, необходимые для решения задач Д.
Согласно первому закону (закону инерции) материальная точка, на которую не действуют силы, находится в состоянии покоя или равномерного прямолинейного движения; изменить это состояние может только действие силы. Второй закон, являющийся основным законом Д., устанавливает, что при действии силы F материальная точка (или поступательно движущееся тело) с массой m получает ускорение w, определяемое равенством
Третьим законом является закон о равенстве действия и противодействия (см. Действия и противодействия закон). Когда к телу приложено несколько сил, F в уравнении (1) означает их равнодействующую. Этот результат следует из закона независимости действия сил, согласно которому при действии на тело нескольких сил каждая из них сообщает телу такое же ускорение, какое она сообщила бы, если бы действовала одна.
В Д. рассматриваются два типа задач, решения которых для материальной точки (или поступательно движущегося тела) находятся с помощью уравнения (1). Задачи первого типа состоят в том, чтобы, зная движение тела, определить действующие на него силы. Классическим примером решения такой задачи является открытие Ньютоном закона всемирного тяготения: зная установленные И. Кеплером на основании обработки результатов наблюдений законы движения планет (см. Кеплера законы), Ньютон показал, что это движение происходит под действием силы, обратно пропорциональной квадрату расстояния между планетой и Солнцем. В технике такие задачи возникают при определении сил, с которыми движущиеся тела действуют на связи, т. е. др. тела, ограничивающие их движение (см. Связи механические), например при определении сил давления колёс на рельсы, а также при нахождении внутренних усилий в различных деталях машин и механизмов, когда законы движения этих машин (механизмов) известны.
Задачи Д. для твёрдого тела (при его непоступательном движении) и различных механических систем решаются с помощью уравнений, которые также получаются как следствия второго закона Д., применяемого к отдельным частицам системы или тела; при этом ещё учитывается равенство сил взаимодействия между этими частицами (третий закон Д.). В частности, таким путём для твёрдого тела, вращающегося вокруг неподвижной оси z, получается уравнение:
где Iz — Момент инерции тела относительно оси вращения, ε — угловое ускорение тела, Mz — Вращающий момент, равный сумме моментов действующих сил относительно оси вращения. Это уравнение позволяет, зная закон вращения, т. е. зависимость ε от времени, найти вращающий момент (задача первого типа) или, зная вращающий момент и начальные условия, т. е. начальное положение тела и начальную угловую скорость, найти закон вращения (задача второго типа).
При изучении движения механических систем часто применяют так называемые общие теоремы Д., которые также могут быть получены как следствия 2-го и 3-го законов Д. К ним относятся теоремы о движении центра масс (или центра инерции) и об изменении количества движения (См. Количество движения), момента количества движения (См. Момент количества движения) и кинетической энергии системы. Иной путь решения задач Д. связан с использованием вместо 2-го закона Д. др. принципов механики (см. Д’ Аламбера принцип (См. Д’Аламбера принцип), Д’ Аламбера — Лагранжа принцип (См. Д’Аламбера — Лагранжа принцип), Вариационные принципы механики) и получаемых с их помощью уравнений движения, в частности Лагранжа уравнений (См. Лагранжа уравнения) механики.
Уравнение (1) и все следствия из него справедливы только при изучении движения по отношению к так называемой инерциальной системе отсчёта (См. Инерциальная система отсчёта), которой для движений внутри солнечной системы с высокой степенью точности является звёздная система (система отсчёта с началом в центре Солнца и осями, направленными на удалённые звёзды), а при решении большинства инженерных задач — система отсчёта, связанная с Землёй. При изучении движения по отношению к неинерциальным системам отсчёта, т. е. системам, связанным с ускоренно движущимися или вращающимися телами, уравнение движения можно также составлять в виде (1), если только к силе F прибавить так называемую переносную и Кориолиса силы (См. Кориолиса сила) инерции (см. Относительное движение). Такие задачи возникают при изучении влияния вращения Земли на движение тел по отношению к земной поверхности, а также при изучении движения различных приборов и устройств, установленных на движущихся объектах (судах, самолётах, ракетах и др.).
Помимо общих методов изучения движения тел под действием сил, в Д. рассматриваются специальные задачи: теория Гироскопа, теория механических колебаний (См. Колебания), теория устойчивости движения (См. Устойчивость движения), теория Удара, механика тела переменной массы (См. Механика тел переменной массы) и др. С помощью законов Д. изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов (см. Упругости теория, Пластичности теория, Гидроаэромеханика, Газовая динамика). Наконец, в результате применения методов Д. к изучению движения конкретных объектов возник ряд специальных дисциплин: Небесная механика, внешняя Баллистика, динамика паровоза, автомобиля, самолёта, Динамика ракет и т.п.
Методы Д., базирующейся на законах Ньютона и называются классической Д., описывают движения самых различных объектов (от молекул до небесных тел), происходящие со скоростями от долей мм/сек до десятков км/сек (скорости ракет и небесных тел), и имеют огромное значение для современного естествознания и техники. Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света; такие движения подчиняются др. законам (см. Квантовая механика, Относительности теория).
в музыке, совокупность явлений, связанных с применением различных степеней силы звучания, громкости. Основные градации силы звучания: piano (в нотах сокращённо р) — тихо, слабо и forte (f) — громко, сильно. Производные от piano в сторону ослабления: pianissimo (рр) — очень тихо, piano-pianissimo (ppp) — чрезвычайно тихо и т.д. (до ррррр); от forte в сторону усиления: fortissimo (ff) — очень громко, forte-fortissimo (fff) — чрезвычайно громко и т.д. (до fffff). Применяются также обозначения mezzo piano (mp) — умеренно тихо и mezzo forte (mf) — умеренно громко. Все эти обозначения относятся к более или менее протяжённым музыкальным отрывкам, в которых выдерживается в общем единая и неизменная степень громкости звучания. Внутри таких отрывков нередко выделяются по громкости отдельные звуки, что обозначается терминами forzato, sforzato и др. (см. Акцент). В музыке широко используется и постепенное усиление или ослабление звучания. Усиление звучания обозначается термином crescendo (cresc, знак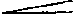 
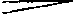
), ослабление — термином decrescendo или diminuendo (decresc. или dim., знак 
). Усиление звучания может вести к новой, более высокой степени выдерживаемой некоторое время громкости, может сменяться ослаблением звучания, образуя вместе с ним динамическую «волну». Для уточнения динамических обозначений к ним могут прибавляться слова meno (меньше, менее), quasi (как бы, подобно), molto (очень), росо (несколько), росо а росо (мало-помалу, постепенно) и т.п.
Градации динамики и их обозначения имеют в музыке лишь относительное значение; абсолютная величина громкости зависит от многих факторов, в том числе от типа инструмента, при ансамблевом исполнении — от количества партий и числа исполнителей на каждую партию, а также от акустических свойств помещения. Так, по абсолютному значению piano на трубе гораздо громче, чем forte вокалиста, громкость звучания piano у целого хора значительно выше, чем у отдельного его участника, и т.п. Абсолютные величины громкости измеряются в акустике и выражаются в фонах (см. Громкость звука).
Динамика – что означает? Определение, значение, примеры употребления
Ищешь, что значит слово динамика? Пытаешься разобраться, что такое динамика? Вот ответ на твой вопрос:
Значение слова «динамика» в словарях русского языка
Динамика это:
Дина́мика (от «сила, мощь») — состояние движения, ход развития, изменение какого-либо явления под влиянием действующих на него факторов.
Динамика
I ж.Раздел механики, изучающий движение тел под воздействием приложенных к ним сил. II ж.
1.Движение, действие, развитие.
2.Состояние движения, ход развития какого-либо явления или процесса.
Динамика
( гр. dynamikos относящийся к силе, сильный)
1) раздел механики, изучающий движение тел в зависимости от действующих на них сил;
2) состояние движения, ход развития, изменение какого-л, явления под влиянием действующих на него факторов (противоп. статика
2);
3) обилие движения, действия.
Динамика
ж.
1) Раздел механики, в котором изучается движение тел под действием приложенных к ним сил.
2) Состояние движения, ход развития какого-л. явления, процесса.
3) Движение, действие, развитие.
Динамика
Динамика
1. раздел механики, изучающий движение тел в зависимости от действующих на них сил;
2. состояние движения, ход развития, изменение какого-л, явления под влиянием действующих на него факторов (противоп. статика
2);
3. обилие движения, действия.
Динамика
Динамика
ход развития, изменения какого-нибудь явления Lib Д. общественного развития. динамика движение, действие, развитие В пьесе много динамики. динамика раздел механики, изучающий движение тел под действием приложенных к ним сил
Динамика
в музыке — различной степени силы звучания, громкости и их изменения. Обозначаются итальянскими терминами: пиано (piano, сокр. p) — тихо; форте (forte, сокр. f) — громко; крещендо (crescendo) — постепенно усиливая; диминуэндо (diminuendo) — постепенно затихая и др. — (от греч. dynamis — сила), раздел механики, в котором изучается движение тел под действием приложенных к ним сил. Основа динамики — Ньютона законы механики.
Динамика
динамика ж.
1) Раздел механики, в котором изучается движение тел под действием приложенных к ним сил.
2) Состояние движения, ход развития какого-л. явления, процесса.
3) Движение, действие, развитие.
Динамика
динамики, мн. нет, ж. (от греч. dynamikos – действующий).
1. Отдел механики, изучающий законы движения тел в зависимости от действующих на них сил (мех.).
2. Ход развития, изменения какого-н. явления под влиянием действующих на него сил; противоп: статика во 2 знач. (науч.). Динамика социального процесса.
3. перен. Обилие движения, действия (книжн.). В пьесе много динамики.
Динамика
1) выражение движения, действия, развития, изменений во времени; описание хода развития какого-либо явления;
2) создание впечатления подвижности художественной формы. Д. может выражаться в ускорении или замедлении ритма лирического, драматического и даже прозаического произведения.
Динамика
ВНЕШНЕТОРГОВЫХЦЕН изменение цен на отдельные товары и целые товарные группы внешней торговли; характеризует экспорт и импорт во внешней торговле отдельных стран, а тж. международную торговлю в целом. Оценка Д.в.ц. осуществляется на основе индексов внешнеторговых цен.
Динамика
ЦИКЛОВПРЕДЛОЖЕНИЯ — частота смены «экспозиции», то есть замены оформления витрин, выкладки товаров, изменения ассортимента с учетом сезонности, праздников.
Динамика
Динамика
Динамика
раздел механики, изучающий движение тел под воздействием сил состояние развития, движения развитие, движение
Где и как употребляется слово «динамика»?
Кроме значения слова «динамика» в словарях, рекомендуем также ознакомиться с примерами предложений и цитат из классической литературы, в которых употребляется слово «динамика».
Так вы сможете гораздо легче понять и запомнить, как правильно употребляется слово «динамика» в тексте и устной речи.
Динамика
Содержание
Содержание
1. Динамика в разных науках
2. Динамика в физике
4. Газовая динамика
Динамика – это состояние движения, ход развития, изменение какого-либо явления под влиянием действующих на него факторов.
Динамика в разных науках
В физике
В астрономии
В науках о Земле
Динамика подземных вод
Динамика русловых потоков
В биологии
Популяционная динамика старения
Динамика растительности (синдинамика) — процесс постепенной трансформации растительных сообществ под действием внешних и внутренних факторов.
В технике
Динамика машин и механизмов
В музыке
Динамика в музыке — совокупность понятий и нотных обозначений, связанных с оттенками громкости звучания.
Динамика в физике
Динамика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия.
Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.
Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.
В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.
Основная задача динамики
Прямая задача динамики: по заданным силам определить характер движения тела.
Обратная задача динамики: по заданному характеру движения определить действующие на тело силы.
Классическая динамика основана на трёх основных законах Ньютона:
1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).
3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
Законы Ньютона в неинерциальных системах отсчета
Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса.
Ряды динамики
Ряды динамики, статистические ряды, характеризующие изменение (развитие) социально-экономических явлений во времени. Например, данные о производстве электричества в СССР за период 1928—73 представляют Ряды динамики
Производство электричества в СССР, млрд. кетЧч
Последовательно расположенные во времени статистические данные называются уровнями Ряды динамики Они должны быть сопоставимы между собой, особенно в территориальном разрезе, по кругу охватываемых объектов, методике расчёта, критической дате, структуре. Уровни Ряды динамики могут характеризовать величину явлении за некоторые отрезки времени (интегральные Ряды динамики) или на определённую дату (моментные Ряды динамики). Анализ Ряды динамики состоит в определении скорости и интенсивности развития рассматриваемого явления, нахождении основные тенденции его развития (тренда), измерении колеблемости уровней, установлении связи с развитием др. явлений, проведении сравнительного анализа развития разных стран или районов. Для анализа Ряды динамики определяются статистические показатели: абсолютные приросты, темпы роста и прироста, средние уровни ряда, средние абсолютные приросты, средние темпы роста и прироста. Абсолютным приростом называют разность между последующим и предыдущим уровнями, а темпом роста — их отношение. Темп прироста составит разность между темпом роста и 1 (в коэффициенте) или 100%. Средний уровень ряда для интервальных рядов определяется как средняя арифметическая, а для моментных рядов — по формуле:
где — средний уровень, y1. — начальный, а уп — конечный, n — число уровней. Средний абсолютный прирост определяется как частное от деления абсолютного прироста за весь период на число единиц времени в периоде. Средний темп роста вычисляется как средняя геометрическая темпов роста за отдельные отрезки времени или как корень, степень которого определяется числом периодов, а под корнем берётся темп роста за весь период.
Определение тренда ведётся выравниванием статистическим. Колеблемость уровней Ряды динамики измеряется средней из квадратов отклонений фактических уровней от тренда. Для установления связи развития данного явления с другими пользуются методом корреляции Ряды динамики, отличающимся от обычного возможностью автокорреляции, авторегрессии, переменной корреляции и временного лага. Для сравнительного анализа разных стран (районов) часто используется приведение к одному основанию, состоящее в определении темпов роста для двух или более стран за одинаковые отрезки времени. Сравнительный анализ развития лучше вести с расчётом показателей на душу населения. Всесторонний анализ Ряды динамики позволяет выявить закономерности развития отражаемых в них явлений.
Газовая динамика
Газовая динамика, раздел гидро-аэромеханики, в котором изучается движение сжимаемых газообразных и жидких сред и их взаимодействие с твёрдыми телами. Как часть физики, Газовая динамика связана с термодинамикой и акустикой.
Фундаментальную роль в формировании Газовая динамика как самостоятельной науки сыграла опубликована в 1902 работа С. А. Чаплыгина «О газовых струях». Развитые в ней методы решения газодинамических задач получили впоследствии широкое распространение и обобщение. Плодотворный метод решения задач Газовая динамика предложили в 1908 нем. учёные Л. Прандтль и Т. Майер, исследовавшие частный случай течения газа с непрерывным увеличением скорости. В 1922 в работе «Опыт гидромеханики сжимаемой жидкости» советский учёный А. А. Фридман заложил основы динамической метеорологии. В 1929 нем. учёными Л. Прандтлем и А. Буземаном был разработан эффективный численно-графический метод решения широкого класса газодинамических задач, распространённый в 1934 сов. учёным Ф. И. Франклем на более сложные случаи течения газа. Эти методы широко применяются при решении задач Газовая динамика с помощью ЭВМ. В 1921 в СССР была создана, а в 1927 оформилась как научное учреждение газодинамическая лаборатория, деятельность которой совместно с Группой изучения реактивного движения (1932) заложила основы сов. ракетной техники.
Задачи газовой динамики при проектировании разнообразных аппаратов, двигателей и газовых машин состоят в определении сил давления и трения, температуры и теплового потока в любой точке поверхности тела или канала, омываемых газом, в любой момент времени. При исследовании распространения газовых струй, взрывных и ударных волн, горения и детонации методами Газовая динамика определяются давление, температура и др. параметры газа во всей области распространения. Изучение поставленных техникой сложных задач превратило современную газовою динамику в науку о движении произвольных смесей газов, которые могут содержать также твёрдые и жидкие частицы (например, выхлопные газы ракетных двигателей на жидком или твёрдом топливе), причём параметры, характеризующие состояние этих газов (давление, температура, плотность, электропроводность и др.), могут изменяться в широких пределах.
Для развития совресенной газовой динамики характерно неразрывное сочетание теоретических методов, использования ЭВМ и постановки сложных аэродинамических и физических экспериментов. Теоретические представления, частично опирающиеся на экспериментальные данные, позволяют описать с помощью уравнений движение газовых смесей сложного состава, в том числе многофазных смесей при наличии физико-химических превращений. Методами прикладной математики разрабатываются эффективные способы решения этих уравнений на ЭВМ. Наконец, из экспериментальных данных определяются необходимые значения физических и химических характеристик, свойственных изучаемой среде и рассматриваемым процессам (коэффициент вязкости и теплопроводности, скорости химических реакций, времена релаксации и др.).
Многие задачи, поставленные современной техникой перед газовой динамикой, пока не могут быть решены расчётно-теоретическими методами, в этих случаях широко пользуются газодинамическими экспериментами, поставленными на основе подобия теории и законов гидродинамического и аэродинамического моделирования. Газодинамические эксперименты в аэрогазодинамических лабораториях проводятся в сверхзвуковых и гиперзвуковых аэродинамических трубах, на баллистических установках, в ударных и импульсных трубах и на др. газодинамических установках специального назначения.
Газодинамические исследования ведутся в тех же научных учреждениях, что и исследования по аэродинамике, а результаты их публикуются в тех же научных журналах и сборниках.