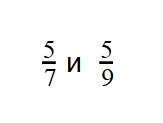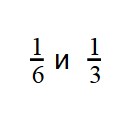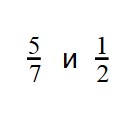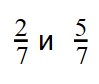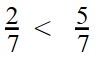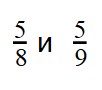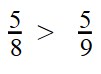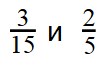Дроби сравнение 5 класс примеры для тренировки

Сравнение дробей: правила, примеры, решения

Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.

Сравнение дробей с одинаковыми знаменателями

Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.

Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.

Сравнение дробей с разными знаменателями

Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.

Если имеются дроби с разными знаменателями, для их сравнения необходимо:

Рассмотрим данные действия на примере.

Ответ: 5 18 > 23 86 .

Сравнение дробей с одинаковыми числителями

Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.

Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.

Рассмотрим на примере.

Решение

Сравнение дроби с натуральным числом

Источник

Тренировочные задания Повторение дробей 5 класс

1. Запишите десятичной дробью:

2. Запишите десятичную дробь в виде обыкновенной (смешанной) дроби:

1) 0,3; 2) 4,9; 3) 3,17; 4) 8,23 5) 3,0001.

3. Запишите обыкновенную дробь в виде десятичной:

1) 7,195 и 12,1; 2) 8,276 и 8,3; 3) 0,76 и 0,7598; 4) 35,2 и 35,02;

5. Выразите в километрах:

1) 2 км 156 м; 2) 5 км 235 м;

6. Выразите в тоннах:

1) 1 т 290 кг; 2) 8 т 685 кг; 3) 624 кг; 4) 8 кг

1) 3,18; 30,625; 164,53; 257,51; 0,61 и 0,28 до единиц;

2) 0,834; 5,453 19,471; 20,263; 6,352; 0,06 и 0,08 до десятых;

3) 0,531; 15,237; 12,467; 0,541; 8,5452 и 0,009 до сотых.

Сложение и вычитание десятичных дробей.

8. Выполните действие:

1) 12,3 + 5,26; 2) 0,48 + 0,057; 3) 15,4 + 3,18; 4) 0,068 + 0,39;

5) 12 + 5,26; 6) 8 + 0,057; 7) 5,4999 + 3,18; 8) 0,068 + 365;

9) 79,1 – 6,08; 10) 96,2 – 4,09; 11) 68,4 – 5,07; 12) 86,3 – 5,07;

13) 5 – 1,63; 14) 6 – 3,54; 15) 8 – 4,83; 16) 7 – 2,78.

Умножение и деление десятичных дробей.

1) 4,35 × 18; 2) 6,25 × 108; 3) 3,85 × 24; 4) 4,75 × 116;

5) 126,385 × 10; 6) 234,166 × 100; 7) 342,581 × 10; 8) 421,273 × 100;

9) 53,3 : 26; 10) 35,7 : 34; 11) 86,1 : 42; 12) 58,8 : 56;

13) 6 : 24; 14) 12 : 16; 15) 7 : 28; 16) 9 : 12;

17) 234,166:10; 18) 421,273:10; 19)126,385:100; 20) 342,581:100.

1) 0,872 × 6,3; 2) 1,6 × 7,625; 3) 0,964 × 7,4; 4) 2,4 × 7,375;

5) 0,045 × 0,1; 6) 0,081 × 0,1; 7) 0,72 × 0,01; 8) 0,69 × 0,01;

9) 0,702 : 0,065; 10) 30,42 : 7,8; 11) 0,0918:0,0085; 12) 25,23 : 8,7;

13) 0,39 : 0,1; 14) 0,83 : 0,1; 15) 0,026 : 0,01; 16) 0,052 : 0,01.

1) 296,2 – 2,7 × 6,6 + 6 : 0,15; 2) 398,6 – 3,8 × 7,7 + 3 : 0,06;

3) 575,4 – 4,3 × 8,8 + 9 : 0,18; 4) 483,6 – 3,6 × 9,9 + 4 : 0,08;

5) 201 – (176,4 : 16,8 + 9,68) × 2,5; 6) (299,3 : 14,6 – 9,62) × 3,5 + 72,2;

7) 161 – (469,7 : 15,4 + 9,52) × 1,5; 8) (534,6 : 13,2 – 9,76) × 4,5 + 61,7.

Основное свойство дроби.

1) 2)

3) 4)

2. Приведите дробь к знаменателю 12:

1) 2) 3) 4) 5) 6) 7) 8)

1) и ; 2) и ; 3) и ; 4) и ;

Глава 5. Сложение и вычитание дробей с разными знаменателями

1. Выполните действия:

1) ; 2) 3) ; 4)

5) ; 6) 7) + ; 8) + ;

9) + ; 10) + ; 11) ; 12)

13) ; 14) 15) ; 16)

17) ; 18) 19) – ; 20) – ;

28) – + ; 29) – + ; 30)

2. Найдите значение выражения:

1) 2) 3) 4)

5) 6) 7) 8)

9) 8 – 3 ; 10) 7 – 4 ; 11) 6 – 2 ; 12) 9 – 5 ;

13) 7 + 1 ; 14) 2 + 3 ; 15) 4 + 1 ; 16) 7 + 2 ;

17) 4 + 5 ; 18) 5 + 1 ; 19) 6 + 2 ; 20) 5 + 2 ;

3. Обратите десятичные дроби в обыкновенные, затем вычислите:

1) 0,5 + ; 2) 0,7 + ; 3) 1,75 + ; 4) 1,5 + ;

4. Обратите обыкновенные дроби в десятичные, затем вычислите:

1) 0,5 + ; 2) 0,7 + ; 3) 1,75 + ; 4) 1,5 + ;

5. Выполните действия:

1) ; 2) ; 3) ; 4) ;

5) ; 6) ;

7) ; 8) .

7. Решите уравнение:

1) b + 5 = 7 ; 2) а – 3 = 4 ;

1) Портниха рассчитывала за 1 ч выкроить платье и за 4 ч сшить его. Однако на всю работу она потратила на 1 ч меньше, чем предполагала. Сколько времени потратила портниха на всю работу?

2) В один вагон планировали загрузить 5 т угля, а в другой 3 т.

Однако всего загрузили на 1 т угля меньше, чем предполагали.

Сколько всего тонн угля загрузили в два вагона?

3) На автомашине планировали перевезти сначала 3 т груза, а потом еще

2 т. Однако перевезли на 1 т меньше, чем предполагали. Сколько

всего тонн груза перевезли на автомашине?

4) С одного опытного участка рассчитывали собрать 3 т пшеницы, а с другого 4 т. Однако с них собрали на 1 т пшеницы больше. Сколько тонн пшеницы собрали с этих участков?

Глава 6. Умножение обыкновенных дробей.

1. Найдите произведение:

1) ; 2) ; 3) × ; 4) ; 5) ; 6) ; 7) × ; 8) × ; 9) ; 10) × ; 11) × ; 12) × ; 17) 2 × 1 ; 18) 1 × 1 ; 19) 1 × 1 ; 20) 1 × 1 ; 21) 3 × 1 ; 22) 3 × 1 ; 23) 2 × 2 ; 24) 5 × 2 ; 25) 1 × 14 ; 26) 2 × 6 ; 27) 2 × 10 ;

Глава 7. Деление обыкновенных дробей.

1) ; 2) ; 3) ; 4) ; 5) : ; 6) : ; 7) : ; 8) : ; 13) 4 : 2 ; 14) 4 : 1 ; 15) 6 : 1 ;

16) 7 : 3 ; 17) 48 : ; 18) 32 : ; 19) 75 : ; 20) 55 : ;

Глава 8. Дробные выражения.

1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7) ; 8) ;

9) ; 10) ; 11) ; 12) .

1. Решите уравнение.

1) 5 : 4 = 25 : у; 2) 3) х : 8 = 1,5 : 2;

4) 5) 6)

7) ; 8) ; 9) ; 10) ;

11) 12) 13) 14)

15) 2 : а = : 16) .

Источник

Сравнение дробей, как правильно

Сравнение дробей с одинаковыми знаменателями

Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.

Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:

Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.

А теперь на примерах.

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.

Давайте разберем наглядный пример сравнения дробей:

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.

Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.

Сравнение дробей с одинаковыми числителями

Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.

Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.

А теперь наши любимые примеры. Погнали!

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Сравнение дробей с разными числителями и разными знаменателями

Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.

Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.

Давайте потренируемся в сравнении дробей.

Пример 1. Сравните дроби:

При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.

Пример 2: Сравните дроби:

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.

Пример 1. Найдите разность:

Вычитаемая дробь меньше уменьшаемой

Пример 2.Найдите разность:

Если знаменатели одинаковые — больше та дробь, числитель которой больше.

Примеры для самопроверки

Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.

Пример 1. Сравните дроби:

Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что

Пример 2. Сравните дроби:

Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что

Пример 3. Сравните дроби:

Ответ:.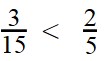

Источник

Карточки-тренажеры можно использовать как обучающие, ликвидации пробелов знаний по теме «Обыкновенные дроби».

Сравнение, сложение и вычитание дробей с одинаковыми знаменателями.

Сравнивай, складывай, вычитай числители.

, так как

Сравнить числа, найти их сумму и разность:

1)и; 2)и; 3)и;

4)и; 5)и; 6)и;

7)и; 8)и; 9)и;

10)и; 11)и; 12)и;

13)и; 14)и; 15)и.

Основное свойство дроби.

Приведение дроби к новому знаменателю:

1.Умножь (или раздели) знаменатель дроби на число.

2.Умножь (или раздели) числитель дроби на то же число.

3.Запиши в ответе получившуюся дробь.

Привести дробь к знаменателю 15.

3) Ответ: .

Привести дробь к знаменателю 7.

3) Ответ: .

1); 6); 11).

Привести дроби к знаменателю 7:

2); 7); 12).

Разделить числитель и знаменатель дроби на 2:

3); 8); 13).

Умножить числитель и знаменатель дроби на 2:

4); 9); 14);

Разделить числитель и знаменатель дроби на возможно большее число:

5); 10); 15).

Сравнение, сложение и вычитание дробей с разными знаменателями.

1) Привести дроби к наименьшему общему знаменателю.

вычесть получившиеся дроби

с одинаковыми знаменателями.

Сравнить и , найти их сумму и разность.

1) = , = ;

2) 9 , то есть

;

+ = + =.

– = – = .

Сравнить дроби, найти их сумму и разность:

1) и ; 9) и ;

2) и ; 10) и ;

3) и ; 11) и ;

4) и ; 12) и ;

5) и ; 13) и ;

6) и ; 14) и ;

Умножь числитель на числитель и знаменатель на знаменатель:

1)

2)

3)

=

Найдите произведение дробей:

1); 2) ;

3) ; 4) ;

5) ; 6) ;

7) ; 8) ;

9) ; 10) ;

Умножь числитель на знаменатель и знаменатель на числитель:

1)

2)

3)

4)

=

5)

Найдите частное дробей:

1); 2) ; 3) ; 4) ; 5) ; 6) ;

7) ; 8) ; 9) ; 10) ; 11) ; 12) ;

13) ; 14) .

Основное свойство пропорции.

Неизвестный крайний член пропорции равен произведению ее средних членов, деленному на известный крайний.

Неизвестный средний член пропорции равен произведению ее крайних членов, деленному на известный средний.

Источник