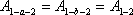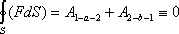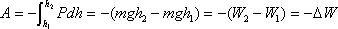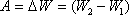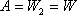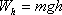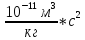какое поле не является потенциальным ответ

Электронная библиотека

В теории поля и ее приложениях рассматриваются так называемые потенциальные поля.

Определение. Поле вектора называется потенциальным, если вектор является градиентом некоторой скалярной функции :

(поле в этом случаи называют также безвихревым или градиентным).

Функция называется потенциальной функцией поля. Часто говорят, что скалярная функция называется скалярным потенциалом поля.

Знак «минус» перед имеет здесь физический смысл, он означает, что в направлении вектора напряженности электрический потенциал убывает (рис. 1.45).

Поле не всякого вектора является потенциальным. Возникает задача: по какому признаку установить, будет ли поле потенциальным? Следующая теорема дает утвердительный ответ и, что важно, приводит к методу нахождения этой функции.

Теорема: Для того чтобы поле было потенциальным, необходимо и достаточно, чтобы вихрь этого поля равнялся нулю:

Отсюда заключаем, что

Что и требовалось доказать.

Это есть условие полного дифференциала функции [6], т.е.

Следовательно, искомая функция (потенциальная) может быть найдена так:

Полный дифференциал функции :

Отсюда поле вектора — потенциально.

Замечание 1. Потенциальное поле обладает рядом особенностей:

б) Циркуляция в потенциальном поле по любому контуру равна нулю.

Это следует из теоремы Стокса:

в) В потенциальном поле криволинейный интеграл не зависит от формы пути интегрирования (доказано при рассмотрении условия независимости криволинейного интеграла от формы пути интегрирования).

При нахождении потенциальной функции в качестве начальной точки берут начало координат, если эта точка принадлежит области, в которой ищется потенциальная функция – это упрощает вычисления; согласно замечанию криволинейный интеграл не зависит от формы пути интегрирования, поэтому удобно брать путь – ломаную (см. рис. 1.46), тогда:

Итог: Криволинейный интеграл потенциального поля на пути равен разности потенциальной функции в конечной и начальной точках этого пути:

другими словами, для потенциального поля имеет место формула Ньютона-Лейбница. Она позволит по известной потенциальной функции найти криволинейный интеграл второго рода (роль первообразной здесь играет потенциальная функция поля ).

Проверить, будет ли поле вектора потенциальным? В случаи его потенциальности найти потенциальную функцию.

Решение. Найдем вихрь этого поля:

Согласно признаку потенциальности поле – потенциальное. Следовательно, существует потенциальная функция, которую найдем, используя формулу (1.115):

В общем случае, если — произвольная точка, то

Задачи для упражнений

2) Будет ли поле вектора потенциальным? В случае потенциальности найти u(х, y, z)

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Источник

Потенциальные и непотенциальные поля. Консервативные и диссипативные силы. Потенциальная энергия.

Силу , действующую на материальную точку, называют консервативной или потенциальной, если работа , совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло:

Изменение направления движения точки вдоль траектории на противоположное вызывает изменение знака консервативной силы, так как величина меняет знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории , например , работа консервативной силы равна нулю.

Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным.

Потенциальные силы создают стационарное поле, в котором работа силы зависит только от начального и конечного положений перемещаемой точки

Работа потенциальной силы при перемещении точки по замкнутой траектории L равна нулю

Если внешние тела, создающие рассматриваемое поле, могут двигаться относительно инерциальной системы, то это поле не будет стационарным. Но нестационарное поле потенциально, если работа, совершаемая силой F при мгновенном переносе точки ее приложения вдоль любой траектории L, равна нулю

К непотенциальным относятся диссипативные и гироскопические силы. Диссипативными силами называются силы, суммарная работа которых при любых перемещениях замкнутой системы всегда отрицательна (например, силы трения). Гироскопическими силами называются силы, зависящие от скорости материальной точки, на которую они действуют, и направленные перпендикулярно к этой скорости (например, сила Лоренца, действующая со стороны магнитного поля на движущуюся в нем заряженную частицу). Работа гироскопических сил всегда равна нулю.

,

знак минус перед интегралом, т.к. сила Р направлена в сторону противоположную изменению h.

Проинтегрируем это выражение:

Эта энергия пойдет на увеличение энергии замкнутой системы тело-Земля т.е. численно равна

Считая поверхности Земли , получим

Источник

Потенциальность электростатического поля

Потенциальное (консервативное) поле − это поле, в котором работа при перемещении зависит только лишь от конечной и начальной точки пути и не зависит от траектории движения тела.

Что такое потенциальное поле

Есть и другое абсолютно равнозначное определение потенциальности поля (консервативной силы).

Известно, что сила гравитации F G

На основе принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.

Легко докажем это математически. Циркуляция вектора напряженности поля точечного заряда E i → по любому замкнутому контуру равняется 0 :

Если поле создает N точечных зарядов, тогда по принципу суперпозиции результирующее поле находим как:

Что такое ротор. Практические задачи

Ротор − это вектор, проекция которого на направление единичного вектора n → определяется таким образом:

Обращаем внимание, что в формуле большой буквой S обозначена площадь, а маленькой буквой s − линейное перемещение.

Ротор описывает интенсивность «завихрения» вектора. На практике при вычислении ротора применяют следующие формулы:

Независимость работы от пути перемещения заряда в электростатическом поле выражается формулой:

где L 1 и L 2 − это различные пути между точками А и В . При замене местами пределов интегрирования получаем:

Выражение ∫ A L 1 B E → · d s → = ∫ A L 2 B E → · d s → представим в виде:

к уравнению выше, получаем:

Это дифференциальная формулировка потенциальности электростатического поля.

Необходимо найти r o t n υ → для точек оси вращения, если υ → − это вектор скорости точек твердого тела, вращающегося с угловой скоростью ω вокруг оси коллинеарной n →

Решение

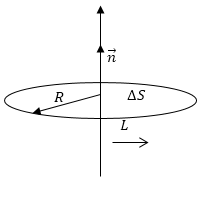
В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рисунок 1 ). Известно, что:

где ∮ d s = 2 π R − это длина окружности.

Необходимо доказать, что из условия потенциальности поля следует: тангенциальные составляющие напряженности электростатического поля непрерывны.

Решение

Поскольку электростатическое поле потенциально, тогда выполняется равенство:

Тангенциальные составляющие − это касательные к произвольной поверхности в любой ее точке. Непрерывность значит, что значения касательных составляющих напряженности одинаковы по обеим сторонам поверхности.

Источник

14. Потенциальные и непотенциальные поля. Консервативные и диссипативные силы. Потенциальная энергия.

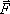
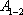
Силу , действующую на материальную точку, называют консервативной или потенциальной, если работа , совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло:

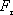
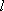
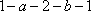
Изменение направления движения точки вдоль траектории на противоположное вызывает изменение знака консервативной силы, так как величина меняет знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории , например , работа консервативной силы равна нулю.

Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным.

Потенциальные силы создают стационарное поле, в котором работа силы зависит только от начального и конечного положений перемещаемой точки

Работа потенциальной силы при перемещении точки по замкнутой траектории L равна нулю

Если внешние тела, создающие рассматриваемое поле, могут двигаться относительно инерциальной системы, то это поле не будет стационарным. Но нестационарное поле потенциально, если работа, совершаемая силой F при мгновенном переносе точки ее приложения вдоль любой траектории L, равна нулю

К непотенциальным относятся диссипативные и гироскопические силы. Диссипативными силами называются силы, суммарная работа которых при любых перемещениях замкнутой системы всегда отрицательна (например, силы трения). Гироскопическими силами называются силы, зависящие от скорости материальной точки, на которую они действуют, и направленные перпендикулярно к этой скорости (например, сила Лоренца, действующая со стороны магнитного поля на движущуюся в нем заряженную частицу). Работа гироскопических сил всегда равна нулю.

,

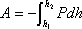
знак минус перед интегралом, т.к. сила Р направлена в сторону противоположную изменению h.

Проинтегрируем это выражение:

Эта энергия пойдет на увеличение энергии замкнутой системы тело-Земля т.е. численно равна

Считая поверхности Земли 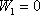, получим

15. Закон всемирного тяготения. Поле тяготения, его напряженность и потенциальная энергия гравитационного взаимодействия.

Между всякими 2 материальными точками действуют силы взаимного притяжения, которые прямо пропорциональны массам точек и обратно пропорциональны квадрату расстояния между ними (закон всемирного тяготения)

Где F- сила взаимного притяжения мат точек, m1 и m2 – их массы, r – расстояние м/у точками, G – гравитационная постоян. = 6,67*

Гравитационное поле (поле тяготения) – один из видов физического поля, посредством которого осущ гравитац взаимодейств (притяжение) тел.

Пример. Солнце и планеты солнечной системы, планеты и их спутники.

Силовой хар-ой полей служит напряженность – векторная величина, где F – сила тяготения, действ на матер точку массой m, помещен в некоторую точку поля. Напряженность гравит поля, создав планетой массу M которой можно считать распределен сферич-симметрич, где r – расстояние от центра планеты до интерес нас точки поля, наход вне планеты.

Потенциалом гравитац поля назыв скалярная величина, где П – потенциальн энергия матер точки массой m, помещен в данную точку поля.

Потенц энергию бесконечно удаленных друг от друга матер точек принято считать = 0.

Источник

Потенциальное поле

Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля. Однако это условие не является достаточным (например, в многосвязной области у безвихревого поля может не существовать скалярный потенциал).

В физике, имеющей дело с силовыми полями, математическое условие потенциальности силового поля можно представить как требование равенства нулю работы при перемещении частицы, на которую действует поле, по замкнутому контуру. В качестве потенциала поля в этом случае можно выбрать работу по перемещению пробной частицы из некоторой произвольно выбранной исходной точки в заданную точку (по определению эта работа не зависит от пути перемещения). Например, потенциальными являются статическое электрическое поле, а также гравитационное поле в ньютоновой теории гравитации.

См. также

Полезное

Смотреть что такое «Потенциальное поле» в других словарях:

потенциальное поле — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN potential field … Справочник технического переводчика

потенциальное поле — potencialinis laukas statusas T sritis Standartizacija ir metrologija apibrėžtis Potencialinės jėgos, išreikštos skaliarine funkcija – potencialo gradientu, laukas, pvz., elektrostatinis laukas. atitikmenys: angl. potential field vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

потенциальное поле — potencialinis laukas statusas T sritis Standartizacija ir metrologija apibrėžtis Skaliarinio potencialo laukas. atitikmenys: angl. potential field vok. Potentialfeld, n rus. потенциальное поле, n pranc. champ potentiel, m … Penkiakalbis aiškinamasis metrologijos terminų žodynas

потенциальное поле — potencialinis laukas statusas T sritis fizika atitikmenys: angl. potential field vok. potenzielles Feld, n rus. потенциальное поле, n pranc. champ potentiel, m … Fizikos terminų žodynas

Потенциальное поле — консервативное поле, векторное поле, циркуляция которого вдоль любой замкнутой траектории равна нулю. Если П. п. силовое поле, то это означает равенство нулю работы сил поля вдоль замкнутой траектории. Для П. п. а (М) существует такая… … Большая советская энциклопедия

векторное потенциальное поле — vektorinis potencialinis laukas statusas T sritis radioelektronika atitikmenys: angl. vector potential field vok. Potentialfeld, n; Vektorpotentialfeld, n rus. векторное потенциальное поле, n pranc. champ vectoriel à potentiel, m … Radioelektronikos terminų žodynas

векторное потенциальное поле — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN vector potential field … Справочник технического переводчика

Потенциальное векторное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном… … Википедия

потенциальное силовое поле — Силовое поле, для которого существует силовая функция. Примечание. Силы в этом силовом поле называются потенциальными силами. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической… … Справочник технического переводчика

Источник