Средняя температура по больнице что значит
Средняя температура по больнице что значит
Виктор тогда шо если одна соседка б—ь, вторая, шов среднем и моя жена тоже.
Если усреднения доводить до абсурда, то можно и так считать.
Выражение современного русского языка, означающее некорректную статистику, когда для создания благополучной картины манипулируют статистическими данными и сравнивают несравниваемые показатели.
полноценный ответ.Спасибо.Наконец поняла что к чему.
Это выражение, насколько я знаю, придумано преподавателями экономико-статистического института в 1960-е годы. Как иллюстрация того, что статистика применима не везде.
она всегда была ложью.Но нужна она,ложь,нам.Почему мы должны жить по законам это лжи,которую придуываем мы сами?
)))) Статистика как наука очень полезна. Например, вся теория измерений строится на статистике. Просто неумелое (часто осознанно неумелое) ее применение несет большие беды.
О микроклимате производственных помещений
Санитарными нормами и правилами СанПиН 2.2.2548-96 «Гигиенические требования к микроклимату производственных помещений» регламентируются требования к микроклимату производственных помещений. Данные правила предназначены для предотвращения неблагоприятного воздействия микроклимата рабочих мест, производственных помещений на самочувствие, функциональное состояние, работоспособность и здоровье человека.
Показателями, характеризующими микроклимат в производственных помещениях, являются:
-температура поверхностей (Учитывается температура поверхностей ограждающих конструкций (стены, потолок, пол), устройств (экраны и т.п.), а также технологического оборудования или ограждающих его устройств)
— относительная влажность воздуха;
— скорость движения воздуха;
— интенсивность теплового облучения.
Существуют оптимальные и допустимые условия микроклимата.
Оптимальные величины показателей микроклимата необходимо соблюдать на рабочих местах производственных помещений, на которых выполняются работы операторского типа, связанные с нервно-эмоциональным напряжением (в кабинах, на пультах и постах управления технологическими процессами, в залах вычислительной техники и др.)
Оптимальные параметры микроклимата на рабочих местах должны соответствовать величинам, приведенным в таблице, применительно к выполнению работ различных категорий в холодный и теплый периоды года.
ОПТИМАЛЬНЫЕ ВЕЛИЧИНЫ ПОКАЗАТЕЛЕЙ МИКРОКЛИМАТА
НА РАБОЧИХ МЕСТАХ ПРОИЗВОДСТВЕННЫХ ПОМЕЩЕНИЙ
Категория работ по уровням энергозатрат, Вт
Температура воздуха, °C
Температура поверхностей, °C
Относительная влажность воздуха, %
Скорость движения воздуха, м/с
Допустимые микроклиматические условия установлены по критериям допустимого теплового и функционального состояния человека на период 8-часовой рабочей смены. Они не вызывают повреждений или нарушений состояния здоровья, но могут приводить к возникновению общих и локальных ощущений теплового дискомфорта, напряжению механизмов терморегуляции, ухудшению самочувствия и понижению работоспособности.
Допустимые величины показателей микроклимата устанавливаются в случаях, когда по технологическим требованиям, техническим и экономически обоснованным причинам не могут быть обеспечены оптимальные величины.
Допустимые величины показателей микроклимата на рабочих местах должны соответствовать значениям, приведенным в таблице применительно к выполнению работ различных категорий в холодный и теплый периоды года.
ДОПУСТИМЫЕ ВЕЛИЧИНЫ ПОКАЗАТЕЛЕЙ МИКРОКЛИМАТА
НА РАБОЧИХ МЕСТАХ ПРОИЗВОДСТВЕННЫХ ПОМЕЩЕНИЙ
Категория работ по уровню энерготрат, Вт
Температура воздуха, °C
Температура поверхностей, °C
Относительная влажность воздуха, %
Скорость движения воздуха, м/с
ниже оптимальных величин
диапазон выше оптимальных величин
для диапазона температур воздуха ниже оптимальных величин, не более
для диапазона температур воздуха выше оптимальных величин, не более
ВРЕМЯ РАБОТЫ ПРИ ТЕМПЕРАТУРЕ ВОЗДУХА НА РАБОЧЕМ МЕСТЕ
ВЫШЕ ДОПУСТИМЫХ ВЕЛИЧИН
В целях защиты работающих от возможного перегревания или охлаждения, при температуре воздуха на рабочих местах выше или ниже допустимых величин, время пребывания на рабочих местах (непрерывно или суммарно за рабочую смену) должно быть ограничено величинами, указанными в таблице.
ВРЕМЯ ПРЕБЫВАНИЯ НА РАБОЧИХ МЕСТАХ
ПРИ ТЕМПЕРАТУРЕ ВОЗДУХА ВЫШЕ ДОПУСТИМЫХ ВЕЛИЧИН
Температура воздуха на
Время пребывания, не более, при
категориях работ, ч
Исполнение данных требований является обязательным для всех предприятий и организаций.
Руководители предприятий, организаций и учреждений вне зависимости от форм собственности и подчиненности в порядке обеспечения производственного контроля обязаны привести рабочие места в соответствие с требованиями к микроклимату, предусмотренными указанными Санитарными правилами.
В соответствие с ч.2 ст. 24 Федерального закона №52-ФЗ «О санитарно-эпидемиологическом благополучии населения» индивидуальные предприниматели и юридические лица обязаны приостановить либо прекратить свою деятельность или работу отдельных цехов, участков, эксплуатацию зданий, сооружений, оборудования, транспорта, выполнение отдельных видов работ и оказание услуг в случаях, если при осуществлении указанных деятельности, работ и услуг нарушаются санитарные правила.
Разграничение работ по категориям осуществляется на основе интенсивности общих энерготрат организма в ккал/ч (Вт).
Так, к категории Iа относятся работы с интенсивностью энерготрат до 120 ккал/ч (до 139 Вт), производимые сидя и сопровождающиеся незначительным физическим напряжением (ряд профессий на предприятиях точного приборо- и машиностроения, на часовом, швейном производствах, в сфере управления и т.п.).
К категории III относятся работы с интенсивностью энерготрат более 250 ккал/ч (более 290 Вт), связанные с постоянными передвижениями, перемещением и переноской значительных (свыше 10 кг) тяжестей и требующие больших физических усилий (ряд профессий в кузнечных цехах с ручной ковкой, литейных цехах с ручной набивкой и заливкой опок машиностроительных и металлургических предприятий и т.п.).
Если Вы не нашли необходимую информацию, попробуйте
зайти на наш старый сайт
Разработка и продвижение сайта – FMF
Почтовый адрес:
Адрес: 350000, г. Краснодар, ул. Рашпилевская, д. 100
Канцелярия +7 (861) 255-11-54
прием посетителей пн., вт., ср., чт. с 10.00 до 16.00
ПТ. и предпраздничные дни с 10.00 до 13.00
перерыв с 13.00 до 13.48
Better Explained: Как правильно посчитать среднюю температуру по больнице
Среднее значение кажется очень простым термином. Именно простота делает его таким лукавым. Давайте поговорим о том, какие средние значения бывают, и как их использовать правильно.
Простой пример: Утром вы ведёте машину до работы со скоростью 30 км/ч, потому что вы не хотите на работу, а обратно едете уже со скоростью 60 км/ч, потому что спешите попасть домой. Какова средняя скорость вашего передвижения в этот день?
Подсказка: Нет, не 45 км/ч.
А пока вот вам небольшая табличка.
Но что всё это значит?
Давайте начнём сначала. Что вообще мы понимаем под словом «среднее»? Для большинства из нас это «какое-то число посередине» либо некое сбалансированное по каким-то критериям число.
Можно предложить более универсальную интерпретацию понятия «среднее значение». Среднее значение какого-либо ряда значений — это то, которым можно заменить любую единицу ряда и получить тот же результат. Условно говоря, я могу выбросить все представленные данные, кроме среднего значения, и общий смысл не изменится.
Одна из целей получения среднего значения — это понять суть выборки данных с помощью репрезентативного образца. Но сам процесс вычисления среднего значения зависит от того, каким образом взаимодействуют элементы группы данных. Давайте посмотрим, как это происходит.
Среднее арифметическое
Среднее арифметическое знакомо нам всем со школы:
среднее арифметическое = сумма всех величин/количество величин
Задачка: вы весите 75 кг и зашли в лифт с подростком весом 50 кг и толстяком весом 175 кг. Каков средний вес вашей группы?
На самом деле вопрос стоит так: Если заменить вашу весёлую компанию тремя клонированными людьми с одинаковым весом, каким весом должен обладать каждый такой клон?
В этом случае мы просто заказываем на фабрике по производству клонов человека трёх экземпляров весом в 100 килограмм каждый (Помним: (75+50+175)/3) и довольно потираем руки.
Преимущества среднего арифметического:
Недостатки среднего арифметического:
Среднее арифметическое срабатывает в 80% случаев. К сожалению, 20% оставшихся случаев и вынуждают нас искать альтернативы для подсчёта среднего значения.
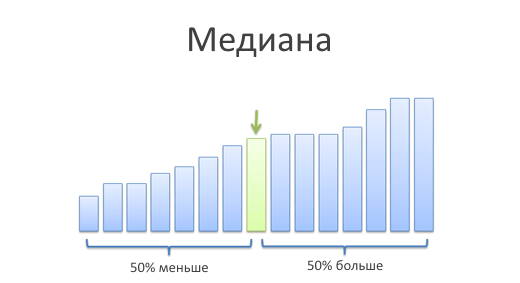
Медиана
Медиана — это та самая грань, которая отделяет наибольшие значения от наименьших. То самое «число посередине». Постойте-постойте, а разве среднее арифметическое делает не то же самое?
Вот вам простой пример. Какое число находится в середине этого ряда?
1, 2, 3, 4, 100
Число «3» находится в середине ряда. И хотя среднее арифметическое (22) является «средним», оно никак не отражает распределения этих чисел. Интуитивно (и абсолютно правильно!) мы считаем, что в середине этого ряда всё-таки 3, а не 22. Здесь среднее значение увеличилось благодаря резко отклоняющемуся от общей массы значению, 100.
Медиана решает эту проблему. Медиана делит наш числовой ряд на две равные части, причём первая половина имеет значения меньше либо равные медиане, а вторая — больше либо равные. Если в середине числового ряда оказывается два числа, мы просто берём среднее арифметическое этих двух чисел, чтобы получить медиану. В числовом ряду 1, 2, 3, 4 медианой станет число 2,5. Именно медиана позволяет выбивающимся из общей массы числам вроде 100 в нашем примере выше не влиять на общее впечатление о числовом ряде.
Преимущества медианы:
Недостатки медианы:
Такие средние значения, как цены на недвижимость или, например, уровень дохода часто вычисляются именно по медиане, потому что нам важна именно средняя стоимость большей части домов в конкретном районе или средний уровень доходов большей части населения. В таком случае Билл Гейтс с годовым доходом в несколько миллиардов не испортит нам всю статистику. Видите, как много зависит от того, как мы работаем с имеющимися данными?
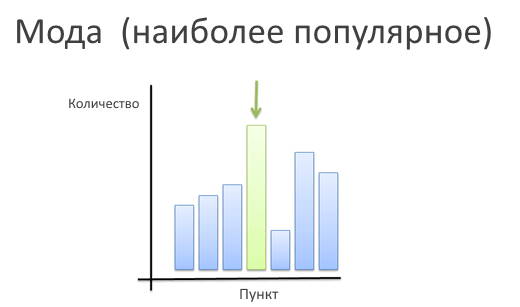
Само слово может звучать странно, но оно означает всего лишь наиболее часто встречающийся в группе элемент. На практике обычно мода определяется путём опросов и сбора мнений. Да, действительно порой бывают случаи, когда лучшим способом получить наиболее репрезентативный образец данных является сбор откликов.
Ну, скажем, вы планируете вечеринку, и вам нужно выбрать день для её проведения. Дни недели — такой же числовой ряд, что и любой другой. Это всего лишь числа от 1 до 7. Среднее арифметическое и медиана тут не помогут (Лиза и Паша могут в пятницу, а Коля и Петя — в воскресенье; поэтому назначим субботу). Что делать в таком случае? Конечно, выбрать тот день, который выберет большинство.
Как правило, мода используется для получения наиболее репрезентативного значения в нечисловых рядах. Популярные цвета в сезоне, хиты продаж, рейтинги фильмов и музыки, лучшие кафе и закусочные определяются именно по моде.
Среднее геометрическое
Наш «усреднённый элемент» зависит от того, что мы делаем с уже существующими элементами группы данных. В большинстве случаев элементы просто складываются, и среднее арифметическое прекрасно работает. Но иногда нам нужно что-то большее. Например, когда мы работаем с инвестициями, площадью и объёмом. В таких случаях данные взаимодействуют между собой именно путём умножения (ожидаемая доходность, объём или площадь фигуры вычисляются с помощью умножения), и это меняет наш подход к выявлению средних значений.
Вот пример. Какой инвестиционный портфель вы предпочтёте? Иными словами, какой из них принесёт большую прибыль в течение типичного года?
Выглядят они похоже. Наша повседневная логика, построенная на привычке к среднему арифметическому, говорит нам, что оба портфеля достаточно рискованны, и оба в среднем приведут к убыткам или нулевой прибыли. Поэтому, наверное, мы выберем портфель Б, поскольку в успешный год он принесёт больше прибыли.
И это неверно! На фондовом рынке с таким подходом мы с вами точно бы прогорели. Проценты с инвестиций умножаются, а не складываются. Мы не можем просто взять и использовать среднее арифметическое, нам нужно найти действительный коэффициент окупаемости. Коэффициент окупаемости считается достаточно просто: берём условные 100% нашего текущего капитала в качестве единицы. Далее представляем колебания доходности-убытка, представленные в описании портфелей, добавляя к нашей единице или вычитая из неё процентные показатели. Затем перемножаем полученные колебания и получаем коэффициент. Для расчёта среднегодового значения коэффициента окупаемости делим полученный коэффициент на 4 (поскольку элементов в нашем числовом ряду четыре).
Коэффициент окупаемости: 1,1 * 0,9 * 1,1 * 0,9 = 0,98 (2% убытка)
Среднегодовое значение: (0,98)^(1/4) = 0,5% годового убытка
Коэффициент окупаемости: 1,3 * 0,7 * 1,3 * 0,7 = 0,83 (17% убытка)
Среднегодовое значение: (0,83)^(1/4) = 4,6% годового убытка
Выбор между 2% или 17%? Огромная разница! Конечно, разумный человек отказался бы от обоих портфелей, но из двух зол лучше выбрать Портфель А. И именно здесь среднее арифметическое не работает.
Несколько примеров, где работает среднее геометрическое:
Среднее геометрическое помогает найти «типичный элемент» среди группы элементов, взаимодействующих друг с другом путём умножения. И, как видим, у него множество практических применений.
Среднее гармоническое
Среднее гармоническое представить сложнее, чем предыдущих представителей «средних», но оно не менее полезно. Между прочим, само понятие «гармоники» в математике связано с обратными числами (1/2, 1/3 и т.д.). Среднее гармоническое помогает нам вычислить среднее арифметическое в рядах чисел, заданных обратными значениями. Это случается чаще, чем вы можете подумать.
Например, если я еду со скоростью 30 км/ч, это значит, что я получаю определённый результат (30 км) за какую-либо единицу времени (1 час). Когда мы хотим узнать среднее значение для нескольких скоростей (Х и Y), нужно думать о результате и единицах измерения, а не об исходных цифрах.
средняя скорость = общий результат/общая единица измерения
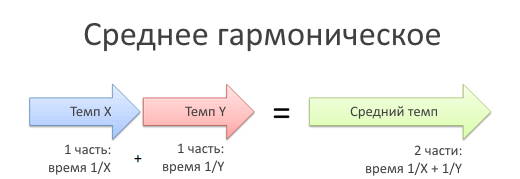
Возьмём двух работников: Х и Y. Оба работают в одном проекте и выполняют одинаковое количество работы, но скорость их работы разная. Какова средняя скорость их работы?
Скажем, работник Х кладёт 30 кирпичей в час, а работник Y — 60 кирпичей в час. Значит, на один кирпич у каждого работника уходит:
Складываем результаты и единицы измерения:
Общий результат: 2 кирпича (Х и Y уложили по одному) Общая единица времени: 1/X + 1/Y (у каждого уходит разное количество времени)
Средней скоростью обоих работников будет:
Если бы у нас было 3 работника (X, Y и Z), их средняя скорость вычислялась бы по формуле:
Здорово же иметь одну формулу вместо того, чтобы каждый раз заниматься долгими вычислениями. Даже вычисляя среднюю скорость 5 нерадивых работников стало бы головной болью. Помните наш первый пример про скорость, с которой вы едете на работу и домой? Чтобы найти среднюю скорость вашего передвижения в тот день, мы просто используем формулу.
При этом нам даже не нужно знать, где находится дом или офис! Теперь вместо X и Y у нас не кирпичи, а количество километров за единицу времени. Вне зависимости от расстояния результат один и тот же: допустим, некое количество километров R мы проходим на скорости X, а другое количество километров R — на скорости Y. Средняя скорость при этом будет вычисляться так же, как вычисляется средняя скорость прохождения 1 км на скорости X и одного километра на скорости Y:
Ключевая идея: Среднее гармоническое используется тогда, когда один и тот же объём работы выполняется на разных скоростях.
Ещё более ключевая идея: Помните, что среднее значение — это один элемент, способный передать суть целой группы элементов. В нашем примере с работой и офисой в среднем туда-обратно мы едем на скорости 40 км/ч (вместо 30 км/ч туда и 60 км/ч обратно). Важно помнить, что средней скоростью мы заменяем каждую «стадию».
Ещё несколько примеров из жизни среднего гармонического:
В чём здесь фокус?
Среднее гармоническое действительно не самая очевидная вещь. Дело в том, что если бы у вас было две разных установки, одна из которых работает со скоростью 10 деталей/час, а другая — 20 деталей/час, конечно, их средняя производительность составляла бы 15 деталей/час. В этом случае вы имеете полное право просто сложить их производительность и вычислить среднее арифметическое, ведь установки работают независимо друг от друга.
Если не верите в среднее гармоническое, можно устроить себе обратную проверку. Мы утверждаем, что наша универсальная установка по заготовке и полировке деталей справляется с 7,14 деталями в час. Проверим: мы знаем, что за час машина либо обрабатывает 25 деталей, либо полирует 10. Получаем:
Подготовка: 7,14/25 = 0,29 часов Полировка: 7,14/10 = 0,71 часов
Да-да, 0,29 + 0,71 = 1, цифры работают: для полного цикла изготовления 7,14 деталей действительно требуется один час.
В качестве заключения
Даже такая простая на первый взгляд идея, как «среднее значение», имеет множество применений. Мы здесь рассмотрели лишь самые основные и не затронули средневзвешенное, центр тяжести, математическое ожидание и многое другое. Но мы поняли главные принципы: