Так называются числа имеющие более двух делителей

Числа. Простые числа.

Натуральные числа, большие единицы и числа, которые не являются простыми, называют составными числами. Т.о., все натуральные числа делятся на 3 класса: единица (имеет 1 делитель), простые числа (имеют 2 делителя) и составные числа (имеют больше 2-х делителей).

Начало последовательности простых чисел выглядит так:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, …

Если представить натуральные числа как произведение простых, то это будет называться разложение на простые либо факторизация числа.

Самое большое простое число, которое известно.

Некоторые свойства простых чисел.

Допустим, p — простое, и p делит ab, тогда p делит a либо b.

Кольцо вычетов Z_n будет называться полем только в случае, если n — простое.

Характеристика всех полей — это нуль либо простое число.

Когда G — конечная группа, у которой порядок |G| делят на p, значит, у G есть элемент порядка p (теорема Коши).

Натуральное p > 1 будет простым лишь в случае, если (p-1)! + 1 можно подулить на p (теорема Вильсона).

Когда n > 1 — натуральное, значит, есть простое p: n 1 — целые взаимно простые числа, содержит нескончаемое число простых чисел (Теорема Дирихле о простых числах в арифметической прогрессии).

Любое простое число, которое большее тройки, можно представить как 6k+1 либо 6k-1, где k — натуральное число. Исходя из этого, когда разность нескольких последовательных простых чисел (при k>1) одинаковая, значит, она точно делится на шесть — к примеру: 251-257-263-269; 199-211-223; 20183-20201-20219.

Теорема Грина-Тао. Есть бесконечные арифметические прогрессии, которые состоят из простых чисел.

Ни одно простое число нельзя представить как n 2k+1 +1, где n>1, k>0. Другими словами, число, которое предшествует простому, не может быть кубом либо более высокой нечётной степенью с основанием, которое больше единицы.

Есть многочлены, у которых множество неотрицательных значений при положительных значениях переменных совпадает с множеством простых чисел. Пример:

Источник

Простые числа

В зависимости от числа делителей среди натуральных чисел различают простые и составные числа.

Простым числом называется такое натуральное число, большее 1, которое имеет только два делителя – единицу и само это число.

Например, число 13 – простое, поскольку у него только два делителя: 1 и 13.

Составным числом называется такое натуральное число, которое имеет более двух делителей.

Так число 4 составное, у него три делителя: 1, 2 и 4.

Число 1 не является ни простым, ни составным числом в связи с тем, что оно имеет только один делитель.

Докажем некоторые свойства простых чисел.

1. Если простое число p делиться на некоторое натуральное число n, отличное от 1, то оно совпадает с n.

Доказательство. Если бы pn, то оно имело бы три делителя: 1, n и p, а тогда оно не было бы простым.

2. Если p и q – различные простые числа, то p не делиться на q.

Доказательство. Так как p – простое, то оно делиться на 1 и само на себя. Но по условию q – простое и pq. Значит, оно делиться на q, на 1 и отлично от 1. Значит, q не является делителем числа p.

3. Если натуральное число a не делиться на простое число p, то a и p взаимно простые.

4. Если произведение двух натуральных чисел a и b делиться на простое число p, то хотя бы одно из них делиться на p.

Доказательство. Предположим, что, а не делиться на p. Тогда по свойству 3 числа а и р взаимно простые. Но так как a

Источник

Простые числа. Составные числа

Определение 1. Простое число − это натуральное число больше единицы, которое делится только на себя и на 1.

Другими словами число является простым, если имеет только два различных натуральных делителя.

Определение 2. Любое натуральное число, которое кроме самого себя и единицы имеет и других делителей, называется составным числом.

Другими словами натуральные числа, не являющиеся простыми числами, называются составными. Из определения 1 следует, что составное число имеет больше двух натуральных делителей. Число 1 не является ни простым, ни составным т.к. имеет только один делитель 1 и, кроме этого многие теоремы относительно простых чисел не имеют места для единицы.

Из определений 1 и 2 следует, что каждое целое положительное число больше 1 является либо простым, либо составным числом.

Ниже представлена программа для отображения простых чисел до 5000. Заполните ячейки, нажмите на кнопку «Создать» и подождите несколько секунд.

Таблица простых чисел

Теорема 1. Любое составное число всегда может быть представлено и притом единственным способом в виде произведения конечного числа простых чисел.

Если k₁ число простое, то k уже представлен в виде произведения простых чисел, в противном случае существует такое простое число p₂, что

Если k₂ число составное, то мы продолжаем процедуру до тех пор, пока k не будет представлено в виде произведения простых чисел:

Первая часть теоремы доказана. Покажем, далее, что разложение составного числа на простые множители единственно (естественно, порядок множителей в произведении может быть другим).

Допустим существует два разложения числа k:

Так как k=p₁p₂p₃. делится на простое число q₁, то по крайней мере один из множителей, например p₁ делится на q₁. Но p₁ простое число и делится только на 1 и на себя. Следовательно p₁=q₁ (т.к. q₁≠1)

Таким образом убеждаемся, что всякое простое число входящее множителем в первое разложение один или несколько раз, входит и во второе разложение минимум столько же раз и наоборот, всякое простое число, которое входит множителем во второе разложение один или несколько раз входит и в первое разложение минимум столько же раз. Следовательно любое простое число входит множителем в оба разложения одинаковое число раз и, таким образом, эти два разложения одинаковы.■

Разложение составного числа k можно записать в следующем виде

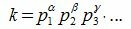(3)

Разложение (3) называется каноническим разложением числа.

Теорема 2. Количество простых чисел бесконечно много.

Доказательство. Предположим, что существует конечное число простых чисел, и пусть наибольшее простое число равно p. Рассмотрим все числа больше p. По предположению утверждения эти числа должны быть составными и должны делится по крайней мере на один из простых чисел. Выберем число, являющиеся произведением всех этих простых чисел плюс 1:

Число z больше p так как 2p уже больше p. p не делится ни на одно из этих простых чисел, т.к. при делении на каждое из них дает остаток 1. Таким образом мы приходим к противоречию. Следовательно существует бесчисленное множество простых чисел.

Данная теорема является частным случаем более общей теоремы:

Теорема 3. Пусть задана арифметическая прогрессия

где d разность арифметической прогрессии, m первый член, и пусть d и m взаимно простые числа. Тогда арифметическая прогрессия (5) содержит бесконечное множество простых чисел.

Нетрудно заметить, что при m=1 и d=1 мы получим теорему 2.

Число и сумма всех делителей числа

Теорема 1 дает возможность определить, делится число m на n, если эти числа разложены на простые множители.

Если m делится на n, то n является кратным m:

Тогда любое простое число, входящее в n, должно входить и в m, поэтому в n не могут входить другие простые множители, которые не входят в m и притом эти простые множители в n входят не более число раз, чем в m.

Справедливо и обратное. Если каждый простой множитель числа n входит по крайней мере столько же раз в число m, то m делится на n.

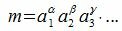Тогда все делители n числа m можно представить формулой

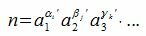(6)

Каждая из чисел n вычисленная формулой (6) является делителем числа m.

Очевидно, при разных значениях i, j, k имеем разные делители числа m. Тогда число всех делителей m равно:

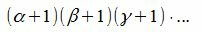Мы доказали следующую теорему:

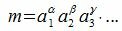каноническое разложение числа m. Тогда число делителей числа m равно:

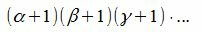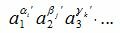
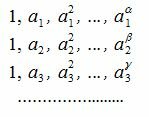Составим все произведения вида , которые различны между собой и являются множеством всех делителей числа m. Найдем сумму этих делителей. Для этого запишем ряды чисел

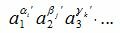
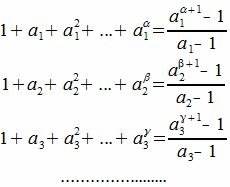Тогда для произведения вида берем по одному множителю из каждого горизонтального ряда. Используя правила умножения многочленов получим:

Заметим, что правая часть каждой строки является суммой членов геометрической прогрессии.

Следовательно сумма всех делителей числа m равна

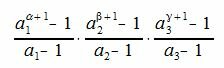(7)

Мы доказали следующую теорему:

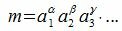каноническое разложение числа m. Тогда сумма всех делителей числа m равна выражению (7).

Источник

Урок 4 Бесплатно Простые и составные числа

На этом уроке мы познакомимся с двумя видами чисел. Они будут различаться количеством делителей.

Также узнаем, как можно разложить составное число на простые числа, изучим основную теорему арифметики и увидим решето Эратосфена.

Простые и составные числа

Если мы попытаемся разделить число 11 на какие-нибудь числа без остатка, то у нас получится это сделать, только если мы будем делить на 1 или на 11.

Получается, что число 11 имеет только два делителя: 1 и 11.

Если мы поступим так же с числами 9 и 18, то узнаем, что у числа 9 три делителя: 1, 3 и 9, а число 18 имеет шесть делителей: 1, 2, 3, 6, 9 и 18

Натуральное число простое, если оно имеет делителями только единицу и само себя.

Если натуральное число имеет больше двух делителей, то оно называется составным.

Таким образом, числа, которые мы используем при счете, в итоге можно разделить на три разные группы по количеству делителей:

Пример 1

Даны числа: 1, 7, 10, 12, 13, 24. Найдите все делители для каждого из чисел. Выпишите числа, имеющие:

В) больше двух делителей

Решение:

Число 1 имеет один делитель: 1

Число 7 имеет два делителя: 1, 7

Число 10 имеет четыре делителя: 1, 2, 5, 10

Число 12 имеет шесть делителей: 1, 2, 3, 4, 6, 12

Число 13 имеет два делителя: 1, 13

Число 24 имеет восемь делителей: 1, 2, 3, 4, 6, 8, 12, 24

Ответ:

А) один делитель- 1

Б) два делителя- 7, 13

В) больше двух делителей- 10, 12, 24

Таким образом, числа 7 и 13 являются простыми, потому что имеют по два делителя.

Числа 10, 12, 24 являются составными, потому что имеют больше двух делителей.

Пример 2

Даны числа: 2, 4, 17, 21, 28, 30, 42, 55, 127. Какие из них простые, а какие составные?

Найдите все делители для составных чисел.

Решение:

Простые: 2, 17, 127

Составные: 4, 21, 28, 30, 42, 55

Число 4 имеет три делителя: 1, 2, 4

Число 21 имеет четыре делителя: 1, 3, 7, 21

Число 28 имеет шесть делителей: 1, 2, 4, 7, 14, 28

Число 30 имеет восемь делителей: 1, 2, 3, 5, 6, 10, 15, 30

Число 42 имеет восемь делителей: 1, 2, 3, 6, 7, 14, 21, 42

Число 55 имеет четыре делителя: 1, 5, 11, 55

У меня есть дополнительная информация к этой части урока!

Простые и составные числа с древнейших времён интересовали разных учёных. Например, древнегреческий учёный Эратосфен (276- 194 гг. до н.э.) занимался вопросом таких чисел.

Он был главой Александрийской библиотеки и в его работах появились первые факты математической географии, вычисления величины земного шара с достаточно для того времени хорошей точностью.

Для своих вычислений он создал довольно простой способ, который использовался для исследования простых чисел и дошел до нашего времени без изменений. Этот способ назвали «Решето Эратосфена».

Пусть перед нами стоит задача нахождения простых чисел от 1 до 100 включительно.

Распишем все эти числа в квадрате 10 на 10.

После этого начинаем зачеркивать те, которые делятся на 2, потом на 3, потом на 5 (на 4 не берем, ведь они уже будут зачёркнуты, когда мы будем зачеркивать делящиеся на 2), потом на 7 и… всё!

Больше зачеркивать ничего не нужно, так как дальше работает доказанное правило: оставшиеся числа в таблице будут простыми.

Почему вдруг такую таблицу назвали решетом?

Получается вот что: мы убираем числа, потом повторяем с оставшимися числами, и то, что будет не зачёркнуто, как бы напоминает то, что ОСТАЕТСЯ В РЕШЕТЕ.

Если внимательно посмотреть на табличку, то можно увидеть что все вычеркнутые стоят на прямых линиях. А, кто видел решето, тот знает, что оно состоит из нитей, натянутых в виде прямых. Значит, можно построить такое решето, просто проводя прямую в тех местах, где число нужно вычеркнуть – вот и все. Поэтому мы и получаем подобие решета.

Решето Эратосфена работает по подобию простой вычислительной машины. И значит, еще очень давно, была изобретена СЧЕТНАЯ МАШИНА.

На сегодняшний день не существует формулы получения любого простого числа, зато еще с древности известно решето Эратосфена. Всё гениальное просто, как говорится в известном афоризме.

На числовой прямой простые числа не имеют никакой закономерности, стоят в хаотичном порядке. Но если мы соберем числовую прямую в решето Эратосфена большого размера, мы их все просеем через него и соберем без исключения и потерь.

Пройти тест и получить оценку можно после входа или регистрации

Источник

Наибольший общий делитель НОД.

Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.

— число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;

— число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.

Кратко наибольший общий делитель чисел a и b записывают так:

Пример: НОД (12; 36) = 12.

Делители чисел в записи решения обозначают большой буквой «Д».

Наибольший общий делитель (НОД), свойства.

Это означает, в частности, что для приведения дроби к несократимому виду надо разделить её числитель и знаменатель на их НОД.

и поэтому представим в виде линейной комбинации чисел m и n:

.

Вычисление наибольшего общего делителя (НОД).

Эффективными способами вычисления НОД двух чисел являются алгоритм Евклида и бинарный алгоритм. Кроме того, значение НОД (m,n) можно легко вычислить, если известно каноническое разложение чисел m и n на простые множители:

где — различные простые числа, а и — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда НОД (m,n) и НОК(m,n) выражаются формулами:

Если чисел более двух: , их НОД находится по следующему алгоритму:

— это и есть искомый НОД.

Также, для того, чтобы найти наибольший общий делитель, можно разложить каждое из заданных чисел на простые множители. Потом выписать отдельно только те множители, которые входят во все заданные числа. Потом перемножаем между собой выписанные числа – результат перемножения и есть наибольший общий делитель.

Разберем пошагово вычисление наибольшего общего делителя:

1. Разложить делители чисел на простые множители:

2. Подчёркиваем одинаковые простые множители в обоих числах:

64 = 2 • 2 • 2 • 2 • 2 • 2

3. Находим произведение одинаковых простых множителей и записываем ответ:

НОД (28; 64) = 2 • 2 = 4

Ответ: НОД (28; 64) = 4

Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».

Первый способ записи НОД:

НОД (48; 36) = 2 • 2 • 3 = 12

Второй способ записи НОД:

Теперь запишем решение поиска НОД в строчку. Найти НОД 10 и 15.

Источник