Так называются две прямые которые при пересечении образуют прямой угол

Геометрия. Урок 2. Углы

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Понятие угла

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Виды углов:

Биссектриса угла

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

∠ A O D = ∠ B O D = ∠ A O B 2

Углы, образованные при пересечении двух прямых

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.

По свойству вертикальных углов:

∠ C O D = ∠ A O B
∠ B O D = ∠ A O C

( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )

По свойству смежных углов:

∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °

Углы, образованные при пересечении двух прямых секущей

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )

Сумма углов многоугольника

Сумма углов произвольного n -угольника вычисляется по формуле:

Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °

Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °

Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

α n = 180 ° ⋅ ( n − 2 ) n

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с углами

Источник

Построй две прямые, которые при пересечении образуют прямой угол?

Построй две прямые, которые при пересечении образуют прямой угол.

Построение при помощи циркуля

Отметь на ней точку А

Проведи вторую окружность того же радиуса с центром В в точке пересечения первой окружности и прямой

При пересечении двух перпендикулярных прямых образуется 1, острый угол 2, замкнутая линия3, прямой угол4, кривая линия5, тупой угол?

При пересечении двух перпендикулярных прямых образуется 1, острый угол 2, замкнутая линия3, прямой угол4, кривая линия5, тупой угол.

Построй квадрат две стороны которого лежат на сторонах данного прямого угла?

Построй квадрат две стороны которого лежат на сторонах данного прямого угла.

Построй квадрат, две стороны которого лежат на сторонах данного прямого угла?

Построй квадрат, две стороны которого лежат на сторонах данного прямого угла.

Построй прямой угол, одна сторона которого проходит через точку А, а другая через точку К?

Построй прямой угол, одна сторона которого проходит через точку А, а другая через точку К.

Стороны треугольника образующие прямой угол 3 см и 5 см, построй треугольник?

Стороны треугольника образующие прямой угол 3 см и 5 см, построй треугольник.

Вспомни и расскажи, как с помощью угольника построить прямой угол?

Вспомни и расскажи, как с помощью угольника построить прямой угол.

Выскажи предположение о том, на каком рисунке при пересечении прямых образуются прямые углы.

Построй две прямые так, чтобы они пересикались под прямым углом и одна из прямых проходила через точку М?

Построй две прямые так, чтобы они пересикались под прямым углом и одна из прямых проходила через точку М.

Помогите пожалуйста?

Построй круг, который будет симметричным относительно данной прямой.

Построй прямоугольник, который будет симметричным относительно данной прямой.

В тетради проведи прямую.

Построй восьмиугольник, который будет симметричным относительно этой прямой.

Прямые линии, при пересечении которых образуется прямой угол, называются?

Прямые линии, при пересечении которых образуется прямой угол, называются?

Первый столбик 76 81 100 Второй столбик 47 55 82.

76, 81, 100, 47, 55, 82.

Источник

Геометрия. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют при пересечении четыре прямых угла.

Теоретический материал для самостоятельного изучения

Ранее вы уже познакомились с прямыми и выяснили, что они могут пересекаться или не пересекаться.

Сегодня мы продолжим изучать пересекающиеся прямые, которые являются перпендикулярными.

Введём понятие «перпендикулярные прямые».

Для этого рассмотрим две пересекающиеся прямые а и b. Они образуют четыре неразвёрнутых угла. Если один из этих углов будет прямой, то остальные тоже будут прямые, т.к.

∠1 и ∠2 – смежные (по определению смежных углов),

∠1 +∠2=180°(по свойству смежных углов),

∠1 =∠ 3 = 90° – вертикальные (по свойству вертикальных углов),

∠2 =∠ 4 = 90° – вертикальные (по свойству вертикальных углов).

Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют при пересечении четыре прямых угла.

Обозначение перпендикулярных прямых:

Построим перпендикулярные прямые.

Для этого воспользуемся чертёжным угольником и линейкой, как изображено на рисунке.

Рассмотрим свойство перпендикулярных прямых.

Две прямые, перпендикулярные к третьей, не пересекаются.

Рассмотрим прямые АА₁ и ВВ₁, перпендикулярные к прямой РQ. Мысленно перегнем плоскость по прямой РQтак, чтобы верхняя часть рисунка наложилась на нижнюю. Так как прямые углы 1 и 2 равны, то луч РА наложится на луч РА₁, аналогично, луч QB наложится на луч QB₁.

Предположим, что прямые АА₁ и ВВ₁пересекаются в точке М.

Мысленно перегнем плоскость по прямой РQ, точка М накладывается на точку М₁.

Через точки М и М₁ проходят две прямые АА₁ и ВВ₁, что неверно. Следовательно, предположение, что прямые АА₁ и ВВ₁ пересекаются в точке М, невозможно (по аксиоме о взаимном расположении точек и прямых), следовательно, прямые АА₁ и ВВ₁ один не пересекаются. Что и требовалось доказать.

Данный метод доказательства называют методом от противного. Суть этого метода заключается в том, что предполагают противоположное тому, что требуется доказать. Исходя из предположения, путём рассуждений приходят к противоречию.

Этим методом можно воспользоваться для доказательства теоремыо единственности перпендикуляра к прямой.

Из точки, не лежащей на прямой, можно провести не более одного перпендикуляра к этой прямой.

Доказательство. Пустьточка не лежит на данной прямой a. Докажем, что из точки A нельзя провести два перпендикуляра к прямой a. Предположим, что из точки A можно провести два перпендикуляра AH и AK к прямой a. Мысленно перегнем плоскость по прямойaтак, чтобы полуплоскость с границей a, содержащая точку A, наложилась на другую полуплоскость. При этом точки H и K остаются на месте, точка A накладывается на некоторую точку B. Получается, что отрезки AH и AK накладываются на отрезки BH и BK.

Углы AHB и AKB – развернутые, так как каждый из них равен сумме двух прямых углов. Поэтому точки A, H и B лежат на одной прямой, и также точки A, K и B лежат на одной прямой.

Таким образом, мы получили, что через точки A и B проходят две прямые AH и AK. Но это невозможно (по аксиоме о взаимном расположении точек и прямых). Следовательно, из точки A можно провести единственный перпендикуляр к прямой а.

Итак, сегодня получили представление о том, что такое перпендикулярные прямые, рассмотрели свойства перпендикулярных прямых, научились строить и обозначать перпендикулярные прямые, узнали о методе доказательства от противного.

Рассмотрим более сложный метод построения прямых углов на местности.

Для построения прямых углов на местности применяют специальные приборы, например, теодолит (в геодезии).

Но самый простой прибор для построения прямых углов на местности – это экер. Он состоит из двух брусков расположенных под углом 90° и укреплённых на треножнике. На концах брусков вбиты гвоздитак, что прямые, проходящие через них, перпендикулярны. Рассмотрим, как с его помощью построить прямые углы. На заданном луче, в нашем случае ОА, устанавливают экер так, что отвес находится точно над точкойО, а направление одного из брусков совпадает с лучом ОА, совмещение помогает осуществить веха, поставленная на луче ОА. Далее провешивают прямую с помощью другого бруска, получается ∠АОВ =90°.

1. Прямые СА и ВD взаимно перпендикулярны и пересекаются в точке О. Луч ОК – проведён из вершины прямого угла АОВ, так что∠КОВ = 52°. Найдите градусную меру ∠АОК.

Решение: нарисуем рисунок, исходя из условия задачи:

2. Прямые СО и ОD взаимно перпендикулярны, найдите ∠МОВ, если ∠МОА = ∠СОА = 25°, ∠ВОD= ∠МОВ.

Решение. Т.к. прямые СО и ОD взаимно перпендикулярны, то ∠СОD = 90°

По условию задачи, ∠МОА = ∠СОА = 25°, ∠ВОD = ∠МОВ.

∠ СОD = ∠МОА + ∠СОА + ∠ВОD + ∠МОВ = 25° + 25° +2·∠МОВ = 50° + 2 · ∠МОВ = 90°

Источник

Параллельность прямых

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Источник

Угол между пересекающимися прямыми: определение, примеры нахождения

Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.

Что такое угол между пересекающимися прямыми

Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.

Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.

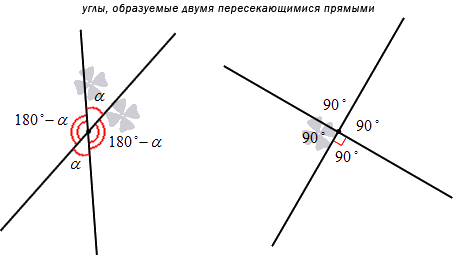
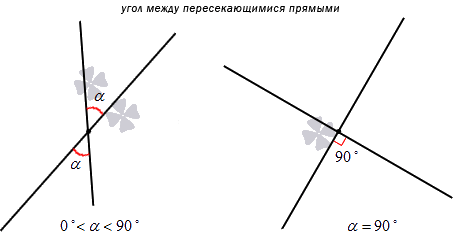
Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.

Взгляните на рисунок:

Перейдем к формулированию основного определения.

Как найти угол между пересекающимися прямыми на плоскости

Умение находить меру угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Метод решения можно выбрать из нескольких вариантов.

Для начала мы можем взять геометрические методы. Если нам известно что-то о дополнительных углах, то можно связать их с нужным нам углом, используя свойства равных или подобных фигур. Например, если мы знаем стороны треугольника и нужно вычислить угол между прямыми, на которых эти стороны расположены, то для решения нам подойдет теорема косинусов. Если у нас в условии есть прямоугольный треугольник, то для подсчетов нам также пригодится знание синуса, косинуса и тангенса угла.

Координатный метод тоже весьма удобен для решения задач такого типа. Поясним, как правильно его использовать.

Начнем с формулировки основного принципа нахождения угла в заданных условиях.

Нам известно, что с понятием прямой линии тесно связаны такие понятия, как направляющий и нормальный вектор. Если у нас есть уравнение некоторой прямой, из него можно взять координаты этих векторов. Мы можем сделать это сразу для двух пересекающихся прямых.

Угол, образуемый двумя пересекающимися прямыми, можно найти с помощью:

Теперь рассмотрим каждый способ отдельно.

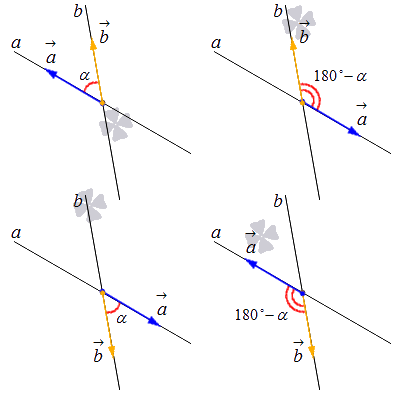
Во втором случае были использованы формулы приведения. Таким образом,

Запишем последнюю формулу словами:

Косинус угла, образованного двумя пересекающимися прямыми, будет равен модулю косинуса угла между его направляющими векторами.

Из нее мы можем вывести формулу косинуса угла между двумя заданными прямыми:

cos α = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2 = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

Тогда сам угол можно найти по следующей формуле:

α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2

Приведем пример решения задачи.

Решение

Ответ: данные прямые образуют угол в 45 градусов.

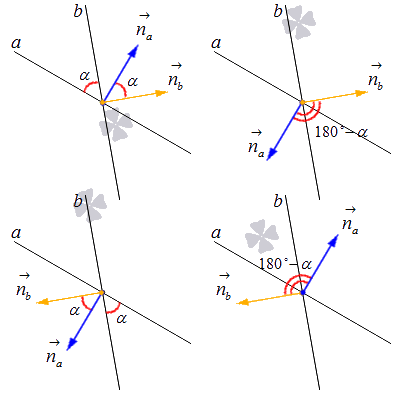
Формулы для вычисления косинуса угла между пересекающимися прямыми и самого этого угла с помощью координат нормальных векторов выглядят так:

Здесь n a → и n b → обозначают нормальные векторы двух заданных прямых.

Решение

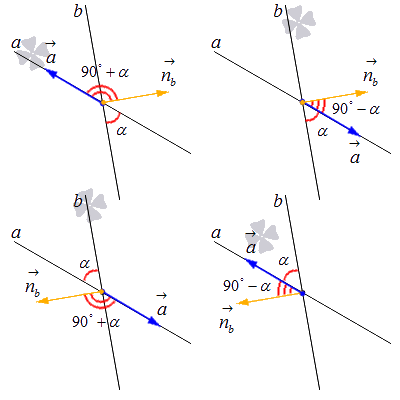
Разберем последний случай – нахождение угла между прямыми, если нам известны координаты направляющего вектора одной прямой и нормального вектора другой.

Если величина угла между заданными векторами не более 90 градусов, получается, что он будет дополнять угол между a и b до прямого угла.

Если он менее 90 градусов, то мы получим следующее:

Используя правило равенства косинусов равных углов, запишем:

Чтобы найти синус угла между двумя прямыми, пересекающимися на плоскости, нужно вычислить модуль косинуса угла между направляющим вектором первой прямой и нормальным вектором второй.

Запишем необходимые формулы. Нахождение синуса угла:

Нахождение самого угла:

α = a r c sin = a x · n b x + a y · n b y a x 2 + a y 2 · n b x 2 + n b y 2

Здесь a → является направляющим вектором первой прямой, а n b → – нормальным вектором второй.

Решение

Обратите внимание, что мы взяли уравнения из предыдущей задачи и получили точно такой же результат, но другим способом.

Ответ: α = a r c sin 7 2 34

Приведем еще один способ нахождения нужного угла с помощью угловых коэффициентов заданных прямых.

Решение

Ответ: α = a r c cos 23 2 34

В выводах этого пункта следует отметить, что приведенные здесь формулы нахождения угла не обязательно учить наизусть. Для этого достаточно знать координаты направляющих и/или нормальных векторов заданных прямых и уметь определять их по разным типам уравнений. А вот формулы для вычисления косинуса угла лучше запомнить или записать.

Как вычислить угол между пересекающимися прямыми в пространстве

Вычисление такого угла можно свести к вычислению координат направляющих векторов и определению величины угла, образованного этими векторами. Для таких примеров используются такие же рассуждения, которые мы приводили до этого.

Для нахождения самого угла нам понадобится эта формула:

α = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Решение

Источник